NOTE: This plain text article interpretation has been digitally created by OCR software to estimate the article text, to help both users and search engines find relevant article content.  To read the actual article text, view or download the PDF above.

Reprinted from Perspectives in Biology and Medicine Vol. VIII, No. 4, Summer 1965 Copyright 1965 by the University of Chicago Printed in U.S.A.

DO WE LIVE IN THE BEST OF ALL WORLDS? SPIDER WEBS SUGGEST AN ANSWER

PETER m WITT*

It has been proven, he said, that things cannot be any different, because, as everything has been created for a purpose, it necessarily happened for the best purpose. Notice that noses were created for wearing glasses, and consequently we have glasses. Legs are obviously made for wearing boots, and we have boots!.. . From all this follows that those who have stated that all is good said something foolish: they should have said that all is best. [Translated from Voltaire, Candide, chap, i, para. 5.]

An insect flies in a zigzag pattern through the air. With its efficient compound eyes it looks for prey. Suddenly its motion is halted by an invisible barrier: the orb web of the garden spider. The animal struggles frantically and thrashes around. Thin threads of the web stretch and rupture. The fly appears nearly free, but at this moment the spider approaches, quickly seizes its prey, bites it with poisonous fangs and, with rapid twirling, wraps the insect with a wide swathing band. Finally the motionless bean-shaped package which is all that is left of the fly is carried to the spider’s hiding place and prepared for consumption.

In observing such a process one sometimes wonders whether things could not have been designed more efficiently. We remember the frequently quoted words of Helmholtz that he would have refused to accept from a mechanic an instrument as poorly built as the human eye. Occasionally we feel an impulse to say: Let me redesign this process so that it serves its purpose more efficiently and with greater economy. Gertsch [1] said about one type of web, “One wonders whether Hyptiotes has not gone to more trouble than the web is worth in producing her triangle

* Address: State University of New York, Upstate Medical Center, Syracuse, N.Y. The original data reported here were obtained during research supported by a grant from the National Science Foundation.

475

trap.” And, “It is true, however, that the same kind of objection to needless efficiency can be leveled against the snare of the typical orb weavers.”

After fifteen years of observing mainly two species of spiders (Zygiella-x-notata and Araneus diadematus) building their geometric orb webs, after measuring and analyzing those webs and trying to interpret changes in the pattern, I have come to the conclusion that my first criticism of the web was based on incomplete knowledge of the problem. I will follow some of the lines of thought that occurred throughout these years in connection with the pattern of the geometric orb web and demonstrate with a specific example evidence for what seems the general rule—namely, that many tendencies are at work in a structure like the orb web and that the final product is a well-balanced compromise between all of them.

The web seems to lend itself better to such an analysis than do many other structures because it can be made visible and measurable. To achieve visibility, white paint is sprayed on the thread pattern which each animal will build daily, provided that yesterday’s web is destroyed. Photographed against a dark background, each strand of the web shows up clearly (Figs. 1-3). The geometry of the pattern reflects the functioning of the builder: size and accuracy as well as proportions can be expressed in figures and interpreted in terms of sensory-motor function. If understanding consists in elucidating the reasons for as well as the purpose of the existence of such a pattern, the following analysis should improve understanding of the orb web.

The Weh as a Trap

A web catches the spider’s food. Flying insects and other prey are held in its meshes. It seems likely that the fly, guided by its sense of vision, does not see the web until it is too late. The threads are very fine and practically invisible in a new web. A diameter is not a meaningful measure: the threads are not circular in cross-section, and dimensions change under tension. But the thickness of the thread can be gauged from the fact that an Araneus diadematus web with about 10 m. of thread weighs not more than about 0.1 mg. (1 microgram of material for 10 cm. of thread). If the web is practically invisible for the prey, it is invisible for the trapper too. Its radial construction, on the other hand, makes it most advantageous for transmitting tension changes and vibration from all parts to the center and allows the spider to move quickly from the center to any part. Watching a

476

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

Spider catching flies in the web, we observe how it makes use of exactly these properties. The orb-web-building spider has a very poor sense of vision [2-5] and a highly developed sense of touch and vibration [6-8] so that it is in no way impeded by the invisibility of the web. One could ask here the unanswerable question: which came first, the spider’s highly developed sense of touch or the web’s invisibility?

Araneus sits in the middle of the trap (Fig. 1); some other species wait on the outside, a signal thread connecting them with the hub (Fig. 2). The moment the web bounces under the impact of the fly, the spider turns in the hub and plucks radii until the sector containing the new weight has been found. Vibration from the movements of the fly provokes further action. The events can be separated experimentally: a glass bead thrown into the web makes the spider attentive, but only after the bead is made to vibrate in resonance to a tuning fork, does the spider attack. The whole structure of the web serves as a means to extend the sense of touch over a wide area; the radii can be regarded as elongated legs transmitting signals from a large region.

The size of the trap limits the amount of prey a spider can catch. Size, however, is limited by several factors: it will be shown later that there is evidence that web size is determined at the outset by the bodily conditions of the spider (weight, contents of the glands, utility of the first two legs). Economy explains the geometry of the pattern: a given mesh width determines the minimum size of the prey which will be safely caught; a regular repetition of that mesh width over a large area is more saving of material than an irregular one. Ease of movement across the web, stability, and orientation probably account for the fact that the web is not built of straight lines crossing equidistantly at right angles, but in a radial structure covered by a spiral.

It is important to consider how the web holds the prey, once caught. The spiral threads (which are thinner than the radii) are covered with glue secreted by a special gland, the aggregate gland [9]. The spiral has to hold the fly, which, through its frantically struggling movements gets more and more entangled in the elastic and partly ruptured threads. But the fly can free itself after a while. The cooperation of the spider is needed. The desperate struggle of the insect gives the spider just enough time to run toward its prey, bite it with its poisonous fangs, and wrap it up. The orb web is not a permanent trap for bigger prey; it needs the active participa-

477

tion of the waiting trapper. The spider’s presence and active contribution toward overpowering its victim constitute a means for keeping the web as delicate and invisible as we find it. A permanent trap would not only have to be heavier and more enduring, but, given the spider’s speed and strength, it would represent more than the minimum provisions necessary to catch food. Eisner and colleagues [io] believe that moths elude capture by virtue of their loose scales, some other insects through their detachable hairs; they apparently get off the glue faster. But according to these observers, even they “do not always escape.”

In the development of the web, all degrees of the spider’s participation in catching the prey are represented. The triangular web of the non-poison-ous Hyptiotes is kept stretched by the animal (Fig. 3) and is released only when the insect is entangled. One web is good for only one fly. Zygiella, on the other end, has a remote hiding place and only the front legs are on the signal thread (Fig. 2). There seems to be a steady evolution toward efficiency of the web as a trap with decreasing participation of the trapper.

Material

Thread consists of a relatively simple polypeptide chain which has outstanding properties of strength and elasticity. Might there be superior thread material, easier to make and with properties more advantageous for web-building?

Any strong organic thread material would have to consist of a long polymere chain of high molecular weight. Animals, with very few exceptions, are not known to make beta linkages, which would be necessary for the construction of a cellulose thread material. On the other hand, there is an abundance of protein synthesis already going on in every cell in the body. Endocrine as well as exocrine glands secrete polypeptides, like insulin or oxytocin or the digestive enzymes of the stomach and pancreas. There seems ample cause in the history of the species for the development of a gland producing protein thread.

The spider’s food provides another source for understanding the nature of silk (if we do not assume that selection of food came after development of silk). The pre-orally digested content of a fly’s body contains partially broken-down proteins and sugars. From such building material new fluid fibroin is readily synthesized in the epithelium of the spinning glands. When radioactive alanine, the main component of silk protein, was fed to

478

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

Fig. 3.—Web of Hyptiotes (cavatus) with spider sitting at left, where the 4 radii meet.

Fig. 5.—Two radii are attached to an auxiliary frame Fig. 6.—Construction of a bridge across an angle, as used repeatedly in thread which forms a bridge across a corner of the radius construction, frame.

Spiders, the label was found in a web built only 12 hours later [11]. In emergencies there is another source of supply for thread material: the normal body constituents of the spider. Several Araneus deprived of food for 10 days went on building large and increasingly wider-meshed webs; a decrease in body weight of 49 per cent during that time indicates that they had used their own tissue as supply [12].

Peakall’s recent experiments [13] suggest that there are one or two regulatory mechanisms for the speed of silk synthesis. When the gland was either emptied by pulling the thread, or a cholinergic mechanism was activated (by the application of physostigmine or carbachol), thread production was speeded up significantly. On the other hand, the same investigator could show that the gradual filling of the gland caused a lower speed of silk synthesis: in the course of a 24-hour period between two web constructions, the epithelium of the empty gland started out to secrete protein rapidly into the lumen, then slowed down, and finally worked at a slow, steady pace. During that time a change from active to resting stage could be observed in the epithelial cells. When the gland was emptied before its time (after 6 hours, for instance), synthesis and secretion were speeded up again. Both mechanisms can be shown to be active also in the isolated gland in vitro. The regulation by acetylcholine-cholinesterase, which plays a role in nerve impulse transmission, points to the possibility of a superimposed central nervous regulation of silk production.

Very little is known about the regulation of thread thickness. The existence of 6 spinnerets makes possible the use of one or several simultaneously. Wilson [14] has located a control valve in the silk duct which may regulate thread thickness. Experiments with spiders to which weights had been added [15] prove that such regulation does exist. Increase of the spiders’ body weight by about 30 per cent through a lead weight on their backs produced thread with twice as much material per unit-length in the next web.

The fibroin thread for the scaffold has very specific properties making it strong enough to hold the fast-moving fly and the heavy spider, respectively, while it is so thin that it is practically invisible. According to Lucas [16], the drag line (which consists of the same material as the scaffolding [9]) of the Araneus diadematus has a tenacity of 7.8 gm/denier as compared to 5.2 for nylon and 3.5 for steel. The figures for extension at break are given by the same author as 31 per cent for the spider, 22 per cent for nylon, and

479

8 per cent for steel. Such comparison shows that the mechanical properties of spiders’ silk compare favorably with the strength and elasticity of the best materials known.

It is important to recall that such outstanding silk is assisted in its catching function by a thin layer of glue. This material is apparently spread from the aggregate glands [9] on the emerging structural spiral thread. The’ thin, glue-covered spiral and the stronger, non-sticky radii support the functional division of the web structure into scaffold and catching components.

Structure

Though threads are fine and practically invisible, the web has to be structurally strong. It must serve the multiple purpose of catching and holding the prey, permitting the spider to run to any part without getting caught (the spider seems not protected against its own glue [10]), and, transmitting tension changes. Structurally the problem is solved through different components, each of which is built with a different type of thread by means of a characteristic movement pattern.

All radii run from the hub to the frame. The center in which they meet requires extra strength. Destruction of one central point of convergence of all radii would cause collapse of the whole web. Radii run, in fact, past one another and come together in a dense little web (Fig. 4). This hub is also the place in which Araneus sits, waiting for prey.

The radii directly around the central area of the web are so close together that no fly can get through. There seems no good reason for building a spiral here, in the so-called free zone. The size of this zone may vary—for instance, under the influence of drugs like mezkalin [17]—but it can always be clearly recognized.

The catching area proper surrounds the free zone and constitutes the main part of the web. Its average size was 255.6 sq. cm. in 169 adult webs as compared to 21.0 sq. cm. of the central area and 100.8 sq. cm. frame area outside the spiral.

The frame serves as peripheral fixation for the radii. It permits the spider to build its web “in the middle of nowhere” without attaching each radius individually to a branch. Its few, strong, nearly straight threads form a structure with few angles. Along these strands the spider can cross from radius to radius in the periphery or leave the web in case of danger. Be-

480

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

tween the angles formed by the frame threads and the almost circular spiral, large open spaces occur: an auxiliary frame-thread provides here fixpoints for the radii (Fig. 5). It has been observed [17] that auxiliary frame-threads and the radii which lead to them are omitted under the influence of a sedative drug. They seem to be of borderline importance only, and their absence does not interfere severely with the function of the web. It is interesting to speculate about the observation that a structural component of relatively minor importance for strength is the first to get lost under the influence of a drug.

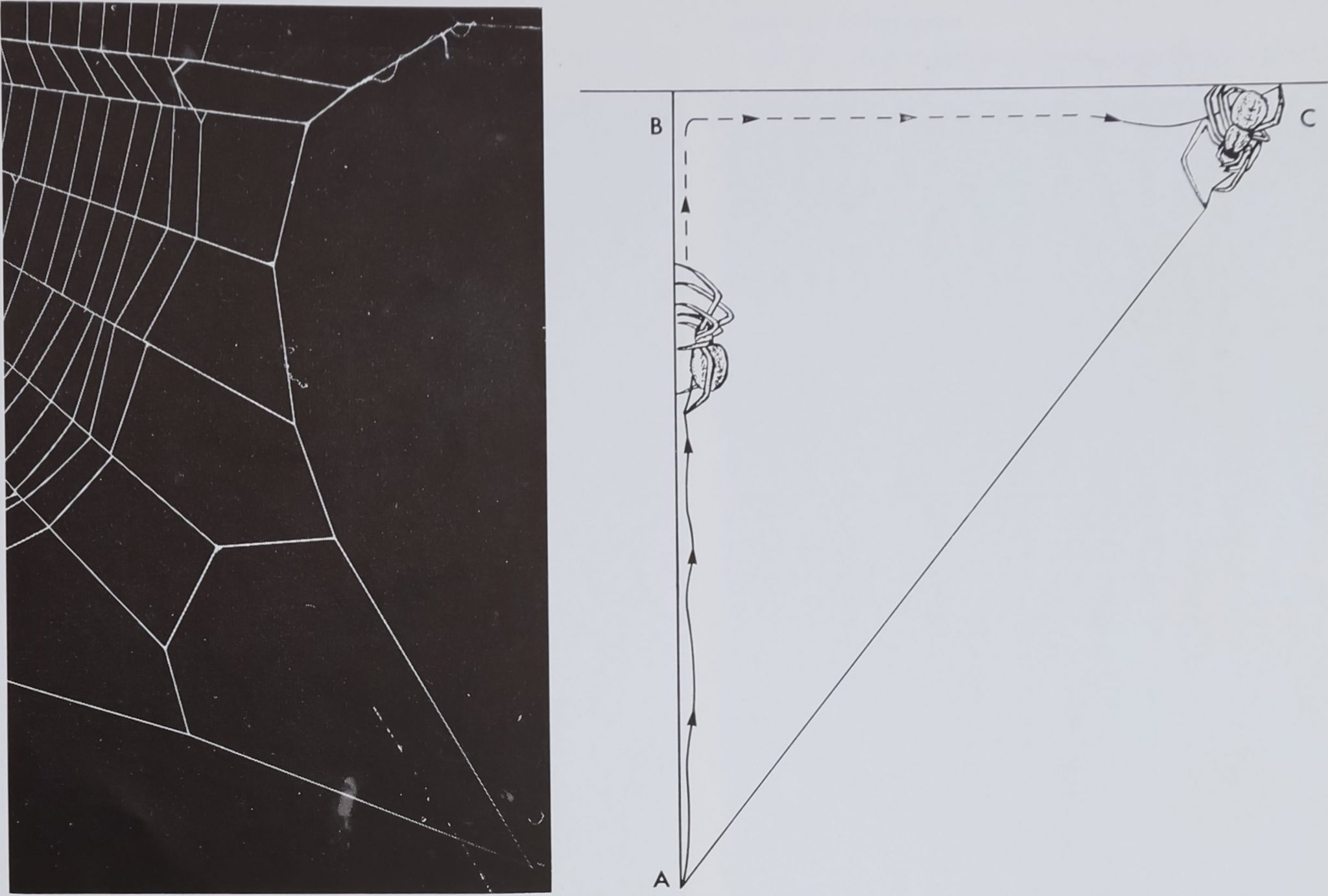
Only very few extra-strong strands fasten the frame to the support in the environment. Frequently we find on top a nearly horizontal bridge, several meters long. This can be built, according to Peters [18], in the very beginning in two possible ways. The spider lets a thread fly until it catches somewhere, than it pulls it straight; or the spider builds a bridge across a fork, as in Figure 6. Each one of the long fastening strands holds only a part of the web. If one thread is cut, only a sector of the web collapses. So far as we know, webs are not built in strong wind. This probably led to claims such as those of Quatremere-Disjonval [19] that weather could be predicted by observing spiders’ web-building.

There is evidence that the structure as a whdle is “planned” at the outset of web-building. Under a variety of circumstances spiders neither ran out of thread nor were they found to have measurable amounts of material left over. For example, two adaptations were observed as a consequence of food deprivation [12J: webs became more widely meshed—i.e., less thread covered the same large area; and body constituents were shifted into thread synthesis. In other observations the size of the web was found related to leg length in growing spiders [20]. When a weight was added to the animal forcing it to build a thicker and consequently shorter thread, a full-sized web with fewer radii and spiral turns was constructed [15]. Experiments of Peters [18] give information on the interrelationship between size of radial angles and spiral distances: the elimination of every other radius leads to a spiral built with turns twice as widely spaced. These and other observations lead to the conclusion that the whole web pattern is predetermined by the first radial angles. At that time the relevant variables seem to be: (1) the amount of thread material stored in the spinning glands (if through physo-stigmine the amount of stored silk is increased 30 per cent [21], the whole pattern is changed); (2) the length of the spider’s legs; and (3) its

481

body weight, which in turn determines thread thickness. From these data the average mesh size or number of subdivisions in the web area is derived. Mesh width in its turn is determined by the size of the radial angles. Such “planning” at the outset obviously adds to the economy as well as the high efficiency of the spider web in this “best of all worlds.”

Web-building as a Movement Pattern

To build the large, intricately patterned orb web must be an effort and an exacting piece of work. The body has to be turned several hundred times to measure all the angles, the front leg stretched again and again to establish the position for each fastening point. An orb web of an adult Araneus diadematus with 39 radii and 35 spiral turns contains, for example, 1,225 points alone where the spiral is fixed to the radii. In addition there are the manifold network in the hub (Fig. 4), the frame, and the auxiliary frame threads (Fig. 5).

Are there any signs of economy in this considerable effort? The question may be answered by examining first the spiral, which requires the greatest labor. Measurement of a typical web, for example, yielded a figure of 17.33 meters for the total length of spiral thread and 5.67 meters for the scaffold (radii and frame). A positive answer is given readily concerning the spiral path itself. It efficiently covers the area available and makes an uninterrupted course from periphery to center without ever crossing or duplicating itself. But the answer is not plain when the intervals of the spiral are considered.

Spiral turns are more widely spaced at the periphery than they are in the interior. Segments of the radii are logarithmically related rather than equal. In terms of the efficiency of the web as a trap, it is difficult to appreciate the basis for this arrangement. On the outside, where radii are farther apart, a narrowly spaced spiral would provide smaller meshes for catching prey; in the interior a wide spacing would seem sufficient. However, when the spider moves from radius to radius, letting out spiral thread and fixing it at each radial crossing, it needs a means of simple orientation as well as economic movement. The hypothesis of the shortest way [22] demands that, where other means of orientation and movement do not interfere, it is easiest to establish the shortest distance from one radius to the next by measuring the perpendicular. This would be particularly convenient in the periphery of the web where radii are far apart. Measurements have shown

482

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

[22] that spiral thread in a web actually runs perpendicular to the next radius. It is concluded that the logarithmic spiral in the orb web, with its seemingly inefficient decreasing distances from periphery to center, points toward economy of movement and simplicity of orientation rather than toward thread economy.

Recently eight consecutive webs of one spider were measured and analyzed [23]. Subsequently the two right front legs were removed and the first six webs constructed after the operation were evaluated. With the help of a computer, eighteen different parameters in the eight pre-operation webs were compared with identical proportions in the six postoperation webs. The post-operation webs were more irregular in angle and spiral construction, the former being considerably more disturbed. Of greatest interest are changes in the three areas of the web: the open frame area outside the spiral; the spiral-covered area; and the central area. While there was no significant change in the size of the frame and central areas of these and many other similarly treated spiders, spiral areas became considerably smaller after delegging. The most likely explanation seemed to be that the six-legged spider, having to work harder to build the web than the eight-legged one, would economize in that part of the web which involved the greatest effort to build. Therefore the animal fabricates a web which is, from the beginning, designed to contain a shorter spiral, while the open center and frame areas stay unaffected. Here, as in the logarithmic form of the spiral pattern, the assumption of an economy of movement provides the simplest explanation for the observed results of the experiments.

While at first glance the geometry of the web appears as the most striking feature, what is most puzzling really are the deviations from the regular pattern. Neighboring central angles between radii, for example, are similar in size, but measurement of such angles in the orbs of 120 adult spiders (about 3,600 angles being evaluated) shows a mean difference of 4.10 degrees between adjacent pairs. The mean difference (or irregularity) of 120 spirals (calculated from about 120,000 measurements) is found to be

0.91 mm. Further increase in angle and spiral regularity may mean a small saving in thread and avoids a few extra-large meshes, but this would have to be achieved by an unproportionate increase in sensory-motor capacity. A conflict between economy of material (perfect regularity) and maximum catching capacity, on the one hand, and economy in sensory-motor

483

control of web-building, on the other, seems to be resolved in the compromise of a not perfectly regular geometric thread pattern. In this connection it is of interest to think about webs built after application of the hallucinatory drug LSD 25: their improved regularity [24] may really constitute a loss in economy of web-construction.

Division of web-building into phases points to a further means of achieving economy in the number of necessary movement patterns. Again there appears a minimum of duplication of thread and movement required to build the thirty-odd radii in the orb web. With the repetition of a relatively simple procedure, the whole scaffold construction is achieved. All except the first three radii seem to be built with the same sequence of movements shown in Figure 6. It consists basically in connecting two points on the arms of an angle by a bridge: starting from A, the spider runs around B to C, letting new thread out all the while and finally pulling it straight across from A to C. By going to the center of the web, the spider can test the angle between existing radii by grabbing them between two front legs. This can be observed during web-building and becomes apparent in delegging experiments also: with one front leg eliminated, the most severe change occurs in angle regularity [23!^^

When the last radius has been completed, a wide-spaced spiral is built from center to periphery. Its function apparently is to provide temporary stability in the web during spiral construction. This auxiliary spiral is later removed.

Movement and orientation during spiral construction are relatively complex and only partly known. Once again there occurs a long and tedious repetition of probably few patterns of movements with slight variations, according to the part of the web. Drug experiments resulting in differential disturbance of upper and lower spiral section as opposed to right and left indicate such differences [25]. No return to radius construction is possible once the spiral has been started [26]. This was shown by Koening, who could make his animals replace destroyed radii while they were still in that building phase. No radius replacement could be brought about after the spiral had been started, however.

The outermost spiral turn is formed of chords stretched between radii. At the periphery, at top and bottom, the distance is too great to permit the spider to climb directly from radius to radius; it has to use a round-about way over the frame or temporary spiral to get across. Here the shortest

484

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

distance can easily be established and serve as guiding rule for the fastening point. On both sides of the web the spider can let herself down on the thread, an assumption which is made likely by the oval shape öf the catching area with the long axis toward gravity. It has also been observed that the animal touches with the outer front leg the last spiral turn before fastening the next one [27]. But beyond these three ways of orientation and movement there must be a considerable number of other means unknown to us. For instance, when the first front leg was eliminated, the spider did not consistently prefer the intact leg on the outside—a maneuver which would have preserved the measuring function. Instead it built irregular spirals and regular ones on different days. Here other means of orientation must have been at work.

In short, the construction of the sticky spiral takes two-thirds of the web-building time; involves the greatest amount of turning, grasping and fastening; and is easily disturbed. This enormously strenuous task seems to be shortened whenever possible.

Conclusions

Among the many possible investigations that might be performed with an experimental tool like the spider web, only very few can actually be carried out. The orb—in its complexity and beauty, its symmetry as well as irregularities, its functionality and sometimes prodigality—seems a prime object for experimentation. Problems ranging from protein synthesis and engineering to the way body movements are regulated supply many challenges to the experimental approach. What guides the decision to follow a specific line of investigation?

Each experiment becomes meaningful if it is based on an over-all hypothesis which it can support, modify, or disprove through its results. Each small piece of investigation fits into a greater pattern and is useful in the large framework. It was in this way that many single observations on web-building behavior, web material and shape, and drug effects began to make sense as I looked at them from the point of view of “the best of all worlds.” This alone seems to me justification for the above approach, even if the guiding hypothesis of either a carefully planning creator or of an unbelievably efficient selection process (which picks out of randomly varying changes only those which serve survival best) does sound strange

to an experimental biologist. I therefore regard this essay as a mental exercise in trying to fit pieces together into an over-all picture.

Its usefulness seems to go beyond the pleasure which we take in working on a puzzle, however: it gives direction to future research. We can proceed to increase our understanding of the working of an animal’s central nervous system; we can apply computer simulation to the investigation of spider web building.¹ When we develop a program for the machine which contains all the means of “planning” and orientation, economy and experience, in mathematical formulations and compare it to the spider web, we may discover that the simulated animal is still far from able to build the web we know. I guess that there are still many unknowns in the beautiful pattern of the geometric orb web which delights the eye on a summer morning and provides much stimulation for human thought.

REFERENCES

1.    W. J. Gertsch. American spiders, p. 154. New York: Van Nostrand Co., 1949.

2.    F. Baltzer. Rev. Suisse Zool., 37:363, 1930.

3.    H. M. Peters. Z. Vergl. Physiol., 15:693, 1931.

4.    B. Hanstroem. Zool. Jahrb. Anat., 59:455, 1935.

5.    T. H. Savory. The biology of spiders, p. 83. London: Sidgwick & Jackson, 1928.

6.    C. Walcott and W. G. VanderKloot. J. Exp. Zool., 141:191, 1959.

7.    M. M. Salpeter and C. Walcott. Exp. Neurol., 2:232, i960.

8.    F. J. Liesenfeld. Biol. Zbl., 80:465,1961.

9.    D. B. Peakall. J. Exp. Zool., 156:345, 1964.

10.    T. Eisner, R. Alsop, and G. Ettershank. Science, 146:1058,1964.

11.    A. L. Breed, V. D. Levine, D. B. Peakall, and P. N. Witt. Behaviour, 23 543,1964.

12.    P. N. Wot. Arch. Environ. Health (Chicago), 7:4, 1963.

13.    D. B. Peakall. J. Exp. Zool., 156:345,1964.

14.    R. S. Wilson. Quart. J. Micr. Sei., 104:557, 1962.

15.    A. Christiansen, R. Baum, and P. N. Wot. J. Pharmacol. Exp. Ther., 136:31, 1962.

16.    F. Lucas. Discovery, Jan. 1964.

17.    P. N. Wot. Die Wirkung von Substanzen auf den Netzbau der Spinne als biologischer Test, p. 44. Heidelberg: Springer-Verlag, 1956.

18.    H. M. Peters. Naturwissenschaften, 27:51, 1939.

¹ Dr. C. F. Reed from the Department of Psychology of Temple University and I have started work on computer simulation of spider web building. As a result of close cooperation between Dr. Reed and me during the last few years, many of his thoughts and suggestions have found their way into these pages and are gratefully acknowledged.

486

Peter N. Witt • Spider Webs

Perspectives in Biology and Medicine • Summer 1965

19.    Quatremere-Disjonval. Araneologie oder Naturgeschichte der Spinnen, p. 42. Frankfurt am Main: Varrentraff und Wenner, 1798.

20.    P. N. Wrrr and R. Baum. Behaviour, 26:309, i960.

21.    P. N. Wrrr. The Pharmacologist, Fall, 1963.

22.    -.    Behaviour,    4:172,1952.

23.    G. F. Reed, P. N. Witt, and R. L. Jones. Behaviour, 25:98, 1965.

24.    P. N. Wrrr. Experientia, 7:310,1951.

25.    C. F. Reed and P. N. Wrrr. In preparation.

26.    M. Koenig. Z. Tierpsychol., 8:463,1951.

27.    M. Jacobi-Kleemann. Z. Vergl. Physiol., 34:606, 1953.

487