NOTE: This plain text article interpretation has been digitally created by OCR software to estimate the article text, to help both users and search engines find relevant article content.  To read the actual article text, view or download the PDF above.

Die Tragheit der pneumatischen Druckubertragnung und Druckverstarkung

W. Wilbrandt, J. L. de la Cuadra und P. N. Witt

Der Mechanismus der Verstärkung ist früher diskutiert und experimentell geprüft worden. Für die Betrachtung wurde ein an der Membran M\ sich einstellendes Kräftegleichgewicht zwischen den Druck-Flächen-Pro-dukten auf der primären und der sekundären Seite der MSbran benützt. Für die Diskussion der Trägheit eignet sich diefjjjpi Grleichgewichtsjbytrach-tung nicht. Es müssen dynamische Größen wie Widerstände und Geschwindigkeit benützt ’werden.. .

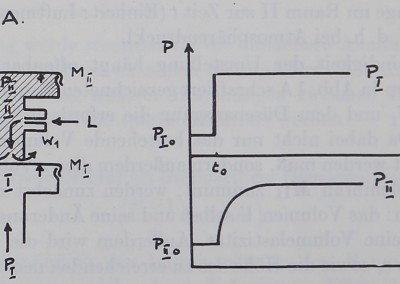
Die Betrachtung geht von folgender Fragestellung aus (Abb. 1B). Das System befinde sich im stationären Zustand, d^feis bestehe ein konstanter Primärdruck Pi₀ und der entsprechende Sekundärdruck Pn₀ habe sich ebenfalls auf Konstanz eingestellt. Nun werde K Primärdruck zur Zejp Null plötzlich fäiif einen höheren Wert’ ^;gehoben, der dann wiederum konstant beibehalthh wird. Nach welcher Gesetzmäßig^® ändert sich dann der Sekundärdruck mit der Zeit, wie rasch strebt ér dem neuen stationären Zustand zu |jjp;

Es sollen folgende Bezeichnungen beni^p ;werdeÄ^^ t H= Zeit nach Éfir Änderung des primären Drucks. v m= Volumgeschwindigkeit (cm³/Sekunden) des Luftstroms im Spalt zwischen Düse und Membran Mi zur Zeit t.

^e^^^iese Geschwindigkeit nach Einstellung des neuen stationären Zu-H Standes.-

Vm= Volumen <lës Baums II z^&¥hen Widerstand* W_v Membran Mn ftpÄ Düsenai^^^^(cm³).

PH= Druck im Baum II S&Zeit V (Atmosphären).

PM= Druck im Baum II zur ZeitlSMo.

PS= Druck im Baum II nach Einstellung des neuensfätionären Zustandes. m^^Bjuftmenge im Baum II zur Zeit t (EinhS: Luftmenge in 1 cm? beim Druck 1, d. l^É|| Atimosphärendruck^^

Die Geschwindigkeit, der Umstellung hängt offenbar davon ab, wie rasch sich in den in Abb. 1A schraffiert gezeichneten Baum II zwischen dem Widerstand W₁ und dem Düsenausgang die erforderliche Luftmenge einführen läßt. Da dabei nicht nur das bestehende Volumen F auf höheren Druck gebracht werden muß, sondern außerdem dieses Volumen durch Vorwölbung der Membran Mn zunimmt, werden zunächst zwei Größen von Bedeutung sein: das Volumen F Selbst und seine Änderung mit dem Druck dF/dP, d. h. seine Volumelastizität. Außerdem wird die Geschwindigkeit des Luftstroms v_e sowie die Höhe des zu erreichenden neuen Drucks P_e von Einfluß sein.

Die Beziehung zwisch^primärem und sekundärem DrucSJ^auf die in der ersten Veröffentlichung eingegangen worden ist, sKffiir die Berechnung nicht berücksichtigt werden. Es soll vielmehr die Höhe des sekundären Drucks im neuen stationären Zustand als gegebep. betrachtet werdem.

Zu einem für die Berechnung verwertbaren Ansatz kann man dann auf

Mechanische Druckverstärkung

173

folgende Weise kommen. Man betrachtet den Spalt zwischen Düsenausgang und Membran Mi als Widerstand W₂, der sich bei Druckvariation verändert. Einfachheitshalber soll er als Funktion nur des Primärdrucks Pi betrachtet werden’ (obwohl« er in Wirklichkeit auch durch den Sekundärdruck beeinflußt wird). Der durch diese Vereinfachung begangene Fehler muß sich in einer zu langsam berechneten Adaptation des Sekundärdrucks äußern. Wäre beispielsweise der Widerstand sofort nach der Erhöhung des primären Druclä unendlich, d. h. würde die Membran vollständig sperren, so würde sich der schraffierte Raum rascher mit Luft anfüllen können, als wenn der Widerstand von Anfang an den definitiven endlichen Wert besitzt, bei dem sich der stationäre Zustand einstellt.

Eine weitere Annahme, die eingeführt werden soll, ist die, daß der Luftraum am Eingang in dën^ Raum-II, d. h. im Widerstand W_1} konstante Geschwindigkeit besitzt. Diese Annahme ist experimentell mit beliebiger Annäherung zu verwirklichen, wenn der Widerstand W₁ und der Druck im Druckreservoirjgenügend gesteigert werden, so daß W_t W₂.

– Eine,letzte].wichtige Frage ist die, wie der Widerstand des Luftspalts zwischen Düse und Membran M_x zu definieren ist. Da der Druck in Atmosphären gemessen wird, kann sein Wert außerhalb des Raums II Hl gesetzt werden. Wäre das Ohmsche Gesetz anwendbar, d. h. wäre die Geschwindigkeit Ël^juitstroms proportional der Druckdifferenz P—1, so wäre die zu

p_j

benützende Widerstandsgröße das Verhältnis-. Da sich jedoch an der

Stelle des- Spaltes der Quersetmitt e für den Luftstrom plötzlich stark ändert, wird eher eine quadratische Beziehung zwischen Geschwindigkeit und Druckdifferenz bestehen, so daß die zu benützende Widerstandsgröße

Die Berechnung werde zunächst für die einfachere Annahme (Gültigkeit des Ohmschen\’|^^^) im einzelnen durchgeführt. Die Änderungen, die sich ;aas der Einführung anderer Beziehungen zwischen Druck und Geschwindigkeit ergebpi, sollen später diskutiert werden.

1st die Geschwindigkeit des Lufteintritts in den Raum II durch den Widerstand W_x konstant (siehe oben), diejenige am Düsenausgang dagegen entsprechend dem Widerstand variabel, so ist die Geschwindigkeit, mit der die Luftmenge im Raum II zunimmt, durch die Differenz der beiden Strömungsgeschwindigkeiten gegeben:

die Form . annehmen würde.

V‘

dm

(1)

Ai Der Druckverlauf bei Gültigkeit des Ohmschen Gesetzes f——- konstant^

dm

HTJr^v^5»

174

W. Wilbrandt, J. L. de la Cuadra uiid P. N. Witt.

(v_e ist gleich der Geschwindigkeit des Eintritts in den Raum II, da ja im stationären Zustand die Geschwindigkeiten im Widerstand W₁ iimÉl im Düsenspalt gleich sind).

Nimmt man an, daß der Widerstand am Düsenausgang sich vom Moment der Änderung des primären Drucks an nicht mehr verändert!(siehe oben), so ergibt sich weiter:

P-lH|P_É -i ‘    ^v    ’

Aus (1) und (2) erhält man

d m H9    I    / Q    \

<⁸>

Um zu einer Gleichung für den zeitlichen Verlauf des Drucks P zu gelangen, muß man nun die Beziehungen zwischen der Luftmenge m und den Größen P und V benütz,en, die .sich ergeben aus dein Gasgesetz:,.

mjmipv    ‘    ^ü

^VdP    ••‘3p.)

sowie aus der Volumelastizität des Raums II:

11• I r    ±W$–h * i Ct    \

IÉIfI“    ,

dVUädP    (6a)

Die Größe a, die reziproke Volumelastizität, werde im folgenden als Vöhiih-nachgiebigkeit bezeichnet. Aus den Gleichungen (5) und (6a) erhält man:

PadP^^mdP

^È{V +.aP)dP.    ‘    (’7)

Setzt man diesen Wert in die Gleichung (3). ein,äj ergibt sich:

■H P—1%

V ~ p^t)

dt M +-a P

m

Integriert man Gleichung (8) unter Benützung der Anfangsbedingung, daß für tm 0 der Druck für P = Pojs^s^ërhäflt, man:”

+^{a Pe) ln} tltlr“ ^(P~ ^Po)] ■    ⁽⁹⁾

Diese Gleichung zeigt zunächst, daß die Geschwindigkeit des Druckanstiegs proportional der Luftströmungsgeschwindigkeit dstV Es ergibt sich weifer> daß sie abnimmt, wenn das Volumen V oder die Volumnachgiebigkeit ‘a steigt, ebenso wenn der Enddruck P_e zunimmt.

Abb. 2 zeigt eine Reihe von berechneten Kurven, entsprechend Gleichung (9) unter Variation der Größen v_e, • V und a.

Mechanische Druck Verstärkung

175

Als zweckmäßiges Maß der Binstellungsgeschwindigkeit eignet sich, die Halbanstiegszeit t_0>5: die Zeit, zu der der Druckanstieg die Hälfte seines definitiven Wertes erreicht hat (Abb. 2). Es gibt sich für diese Größe die Beziehung:

(10b)

Pe^Pn

Für praktische Zwépfie kann man im allgemeinen den Ausdruck

¹) gegenüber 0,69P_e vernachlässigen, sofern nämlich der Druckanstieg’hm? ilaum II ein kleiner Bruchteil einer Atmosphäre ist. Unter diesen Ipmâtänclek^nimmt die^fejchung (10a) eine einfachere Form an:

mK/gr- • 0,694.(01*).    (11)

Die Halbanstiegszeit Wird dann unmittelbar proportional dem definitiv erreichten Überdruck, umgekehrt proportional der Luftströmungsgeschwindigkeit und proportional der Größe (Fill a).

Die Trägheit der Übertragung’ bzw. Verstärkung läßt sich demnach vermindern ersfensL durch Vergrößerung der Strömungsgeschwindigkeit, zweitens durch Verwendung niedriger Enddrucke und schließlich durch Arbeiten mit einem kleinen Wert für (F + «).

Dabei ist wichtig, daß von den

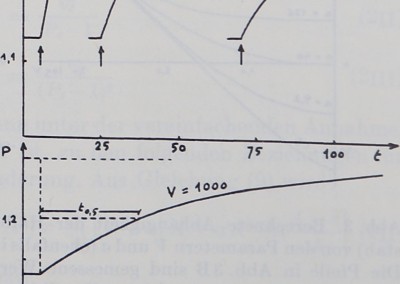
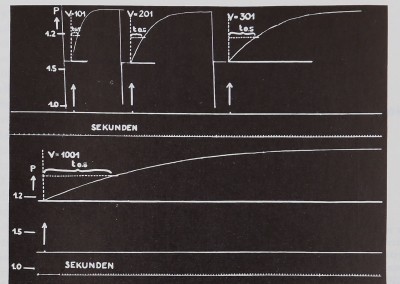
Abb. 2. Berechnete Einstellkurven bei Variation tdes/Volumens V. Für ;:<<Ée anderen Parameter wurden folgende Werte gewählt jSB®., 3,    =:

5,13,    P₀Hl,13i (ent

sprechend den Werten bei den Messungen in Abb. 5). Ordinate: sekundärer Druck. Abszisse: Zeit. Bei der Einstellkurve für V = 1000 ist die’ Halbanstiegszeit £0,5 eingezeichnet. I

0,694—a ²1    (10)

’    v_e    L    2 : J

oder

(10a)

Ve I    \    z;\

Ist der Druck    so    wird    aus    (10a):

mMHHB 0,5)].    (10b)

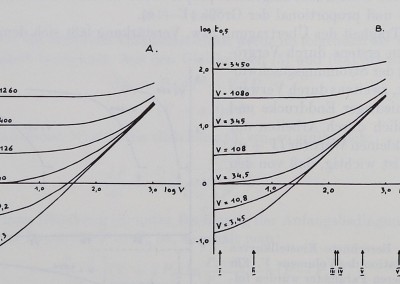
Größen. V und a häufig die ^M^ffidé’Bandére ‘.éorösinierlij’iwkd⁵.⁵ Jn%dièsëm Fall ist praktisch nur eineÄnderungtfc domihâèreSEènfB^ei^èhFinfhiß auf die Trägheit. Arbeitet man ÄiiSjhelsweiseÄ^faiiem VölumeiE®on 10 cm³ und einem Wert für a von M0^ém³^^^®p%äre^ “stöuwird man durch eine Herabsetzung des Volumens 10 auf 1 cm³ fast nichtslli^eijhgn, nämlich nur eine Erhöhung der Einstëllgeschwindi^èit im Verhältnis 110: 101, d. h. um 9%. Abb. 3 zeigt das gleiche in anderer Form: die theoretischen Eufil®! für £_0j5 (in logarithmischem Maßstab) als Funktion von._F bzw. a (ebenfal^H logarithmisch) verlaufen in Ä-.entsprechenden Gebi^Sprakti’sch waag-recht.

Diese Verhältnisse sind auch von Bedeutung für die naheliegende Fragë-, ob sich die Trägheit der Übertragung wesentlich ^vermindern läßt;*d«ëh Verwendung von Wasser als inkoi^n^ssibler Flüssigkeiten Stelle ^n ifiBl In diesem Falle fällt die^GröwlMaüs der Glrachung herfte$ünd di^ Halbanstiegszeit’ ^ist (nebe^^S.^rvor der Klamm^^nm^eh’ Gfoßfen) aiur hoch abhängig /von a. Eine Heräibsetzudg-tder rTEäghëll^ü^dâ^^iünter jÄsga Umständer^isomur dann erzielenlassenl/iWenn-V dominiert. ist es.;’experimentell leiëhf*, den Wer^^M^^^^^^^^Sals den Werket. Die V$f*wëndung von Was^^wiÄliè^al^^^ffi v^rnfetMhamr dann ISfü^pa Yersprechen, wenn man aus irgendeinem Grund, gezwungen ist^ mit reinem großen F zu arbeiten, ^ B.,|)ei;uny^mi(^^er großer räumlicher Ent-

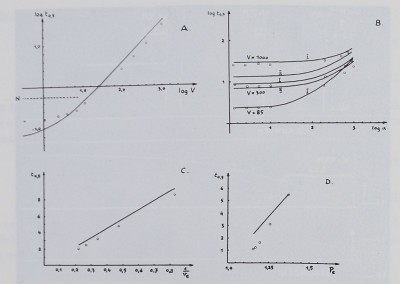
Abb. 3. Berechnete Abhängigkeit der Hälbanstiegszeit! (in logärithmisteherh Maß-stab) von den Parametern V und a (ebenfalls in logarithräischèm Maßstab gezeichiiët). Die Pfeile in Abb. 3B sind gemessene Werte einiger im LaboratoriumiplfoMänch.-licher Druckmesser:    -feines    Kapillarquecksilbermanometei*;    II:    Que^ksdèb.e%?-

manometer 4 mm Durchmesser,; III: Wassermanometer 6 mm Durchmesser; IV: Marey-Kapsel mit .Fahrradschlauchgummi; V: Marey-Kapsel mit Zahnarztplattengummi ; VI: Marey-Kapsel mit Condomgummi. Die vielgebräuchlicheri Marey-Kapseln haben selbst bei-dicken Gummimembranen sehr hohe Wértfë von a!

176    W.    Wilbrandt,    J.    L-.IÉ^MCuadra    und    P.    N.

Mechanische Druckverstärkung

177

f ernung zwischen Mi und Mn. Der Nutzen würde dann aber dadurch stark herabgesetzt, daß es mit Wasser schwieriger ist, große Werte von v_e zu erreichen. Man müßtefdäzu auf jeden Fall die Dimensionierung der Apparatur ^^^MÜcl|3^Eää!dern.

Dagegen ^^^Manii unter-IUmständen möglich, den größten Teil des Baumes II mit Wasser zu füllen und nur den Durchlaß zwischen W_x und der Düse für Luft frei#mMlë^B^ömit man’ebenfalls praktisch unabhängig von V wird. Bei großen Querschnitten fzur Verminderung der nötigen’Beschleunigung der Wasl^ma^p kann man so gelegentlich die Trägheit wirksam herabsetzen.

-!. Ersetzt man die einfache Annahme, der Gültigkeit des Ohmschen Gesetzes durchwandere Bezie^ngepzwischen Drucl^nm Luftströmungsgeschwindig-keit, s<y$eoj»ben sich zunächst bei der Bechnung ^;«cheinbar beträchtliche Differenzen ißi Kesultat (Gleichungen 9, siehe unten), die ;si6h jedoch mit Bmgjauf    .nicht    sehr wesentlich erweisen. Die Ab

hängigkeit dä Halbanstiegszeit¹ von den experimentellen Größen bll&t qualitativ diè gleiche und ändéifPsich auch    ÄfeÜÉii“

lieh?⁵😕

^^^’^urde^^tDiur die^öb,eh_; erwähnte. . Beziehung    konstant

benützt, die als II bezeichnet werde’^sondern aiieh die Form    kon-

V

stantj(III).

Die Änderung betrifft zunächst die Gleichung (2), die folgende Formen pihimmt:

(P-lj.2;:* . (P;₇-1)2    ^v    ‘

Die weitere Entwicklung führt dann untèr der vereinfachenden Annahme, daß wie in Gleichung (10b) P₀ Hl ist, zu den folgenden Beziehungen für den zeitlichen Verlauf der Druckänderung. Aus Gleichung (9) wird:

-Bruck und °d^er    konstant)

B™^B0|    (2ii)

Pe-l    ^v ‘

^t — ~~ [^4³+^Y    (^V + ^a+^²)# + ({7-f a}y4 + a^.³)^F^— (9ii)

wo JgJ’P—1 udjI j|^i= P_ell, bzw.

, A² rJK a – HU , a, A² 1    /n    \

^(9m)

\Wö8E P—1 und A f^j

178

W. Wilbrandt, J. L. de la Cuadra und P. N. Wifft

Die der Gleichung (10) entsprechenden Beziehungen werden:

«w [°.⁸¹⁷ KmWW)] (ion)

%

<„,₅    [uo ⁽jf-,S®)Se,m«j⁽p«Tia)]. dom)

Für kleine Werte von (P_e—1) vereinfachen sich diese Gleichungen wieder wie oben und nehmen die mit der Gleichung (11) bis auf den Wert der Konstanten identische Form an:..

Es ergibt sich also, daß die ‘Halbahpbiëgszeit bei allen’drei Annahmen’^rdie gleiche Abhängigkeit vom den experimentellen Größen* zeigt ‘ünd sich nur um einen konstanter!-Faktor

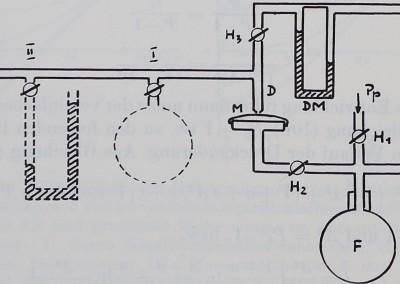
C. Experimentelle Prüfung dér^^^mmmn nèzißliungen Zur experimentellen Prüfung der abgeleit^l^Gleichungen wurde eine Anordnung benützt, die in Abb. 4 schematises wiedergegeben^Pffl Um rasche Änderungen des primären Drucks erzielen zu können (der wieder auf die Membran M wirkt), sind die Hahnen H_x und H₂ eingeschaltet. Durch H_x kann die Flasche F auf einen gewünschten Druckwert ängëfüllt Werden, der am Manometer Ma ablesbar ist. Das Volumen der Flasche F (3,1).,ist gegenüber dem Volumen der Druckkapsel M so groß, daß durch Öffnen des Hahns H₂ (H₁ ist nun geschlossen), der in F herrschende Druck rasch und ohne Absinkendies; Miveaus «1 die Kapsel M âbèfiiäigeii! werdifs kann.

Abb. 4. Schema der Anordnung zur experimentellen Prüfung der Einstellungs-geschwindigkeit. Erklärungen im    b

I    + a)    ■

J-jkzl fagS’VwM;.

■ V_e

Auf der sekundären Séite^dient’mfer Hahn H_z als Variabler Widerstand W_1} Mt dem die Geschwindigkeit ff| modifiziert werden kann. Sie wird an einfem Differentialmanometer DM abgelesen. Zur Variation des Volumens V untfcier Volumennachgiebigkeit a sind zwischen der Düse D und dem regi-slnerendeh Manometer RM an den Stellen I und II Seitenansätze angebracht. Bei I können variable Volumina, ‘V‘ m Form von Flaschenräumen angesetzt Werden, bei II variable Werte von a in Form von U-Rohr-Manometern mit variabler Flüssigkeit und variablem Querschnitt. Das registrierende Manometer RM war ein Quecksilbermanometer, mit dem der Druck ÉB-Iiißkvmogranhion registriert wurde.

‘Âbb. 5 zeigt Beispiele von Registrierungen des Druckanstieges im Raum II bei Variation von V. Die Halbanstiegszeiten zeigen qualitativ die erwarteten lAMerüügëâ, entsprechend den berechneten Kurven der Abb. 2. ^v Um die Gleichungen (10) quantitativ zu prüfen, wurden in Abb. 6 die Weilte* von ^ g’r’aus solchen*]Versuchen sowie aus anderen mit Variation von V, h, P& und gegen die variierten Größen (bzw. ihre Logarithmen) aufgetragen. Die für die experimentellen Werte von P_e,. v_e‘j V und a nach Gleichung (10) berechneten Kurven sind ebenfalls eingezeichnet.

Die Übereinstimmung ist im ganzen gut. Variation von V, a und v_e ergeben Werte etwa entsprechend der Berechnung. Bei P_e, sind die Abweichungen größer.

Mechanische Druckverstärkung    179

Abb. 5.^Beispiele registrierter Einstellkurven, die mit’äer inoAbb. 4 wiedergegebenen Vorrichtung’ gewönnen’ wurden. Abszisse*: Zeit in Sekunden. Ordinate: Sekundärer Drü<fi|sVäriiert wurde das Volumen V, dessen Werte an deh Kurven angegeben wird.

Abb. 6. Vergleich der gemessenen Halbanstiegszeiten (Kreise) Imit den für die entsprechenden Parameterwerte berechneten Kurven (ansgezogen). A: Variation B: Variation von a; C: Variation von    Variation von P_e. Die in. A efim!-

gezeichnete gestrichelte Linie entspricht der halben Schwingungsdauer des verwendeten Quecksilbermanometers. In B sind für F = 300 drei berechnete Kurven gezeichnet, die sich in der Form des Widerstands unterscheiden (siehe Text). I Bespricht dem Ohmschen Gesetz

Für die Variation von a (Abb. 6B) sind drei, berechnete Kurven entsprechend den Gleichungen (11), (llii) und (Hin) eingezeichnet (I, II, III). Die gemessenen Punkte liegen zwischen I und III. Auch in den anderen Versuchsreihen liegen sie tiefer als I.

Vermutlich ist das nicht darauf zurückzuführen, daß dle_f Annahme III /IZz:¹)— konstant\ die Strömungsverhältnisse am Düsenausgang am besten

wiedergibt. Sie werden eher der Annahme II ~ konstant|_T erLtsprechen.

Wahrscheinlicher ist, daß die oben diskutierte vereinfachende Annahme eines zeitlich konstanten Widerstandes verantwortlich ist.. Sie? [muß, wie oben diskutiert, zu Werten t_{0 5} führen, die zu hoch sind.

In den Versuchen der Abb. 6 wurde ein relativ träges System benützt. Bei den kleinsten Werten von V (Abb. 6A) geht offenbar die Bolle ides limitierenden Faktors von der Auffüllung des Raums II an die träge Masse des verwendeten Quecksilbermanometers über: die Halbanstiegszeiten in der Nähe der Schwingungszeit des Manometers folgen nicht mehr desif berechneten Kurve, sondern werden hier konstant.

Kürzere Zeiten lassen sich mit optischer Registrierung erreichen. Abb. 7

jgQ    w.    Wilbrandt,    J.    L.    de    la    Cuadra    und    P.    N.    Witt

Mechanische Druckverstärkung

181

zeigt eine Kurve, die E. Lopez-Botet³ beim Ausbau    Registriermethode    für    den

Broncbialwiderstand bei kleinen Tieren gewonnen bat. Hier wurden V und a^: in der Größenordnung von 1 gehaltén. Die gemessene Halbanltiegszeit ist etwat’ife Sekunde.

^rayHa>igeiid.e Weise ein Versuch uiilfelÉ^^É^ die ^experimen|||| unter günstigsten Bedingungen erreichbare Einstellgescbwindigkeit approximativ zu èr-

Als, Membran, dä&der Membran M\ in dér;

Abb. 1 entsprechen würde, wurde die Mem-‘ hranBaes Lautsprechers verwendet, der von einèm Frequenzgenérator (Philips) mit variablen Frequenzen gespeist wurde. Mit optischer Registrierung des Drucks im Raum II wurde geprüft, bis zu welch® Frequenzen das übertragene Sp^^M’fdeiÜM^mbranschwan-kungèn^an.dër Membran M\ zu folgen imstande; istf. AuMdie photographische Aufnahme der optischen Ausschläge wurde verzichtet, da bei den ho&l^rerwendeten Freaueilpllldie Breite des entworfenen Bandes, die die Amplitude der Schwingungen wiedelgibt und die die einzige interessierende Größe ist, bequem ausgemessen werden konnte.-

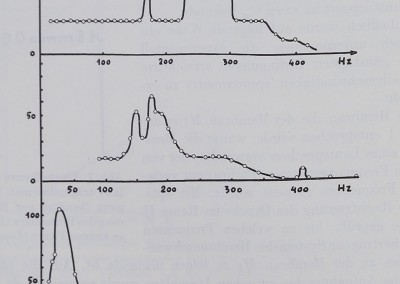
Abb.    Frequenzlfüf^ehV’die    so*g^w^Mien    wurden.    Sie    zeigen,

aufgelägeft auf eme basale Amplitude, die bisr:uber 300 .Hertz konstant bl^ft%nd den Wert Null in einem Fall    900    Hertz    erreicht,    Maxima

an verschiedenen Stellen, die sich mit den experimentellen Bedingungen verschieben^ und im Yerlau£,jver§nd^m_(V Diese Maxima sind offenbar durch Ipwisse Eigenfrequenzen der Apparatur bestimm®die sich nicht vermeid    durch    Veränderung    der    Bedingungen    verschieben    lassen.

Richtig ist,. daß die basale Frequenz bis über 300 Hertz konstant bleiben kann und daß Ausschläge, wenn auch nicht konstant, d. h. amplitudengetreu, bi4zu 800-900 Hertz nachweisbar bleiben können.

Die Werte .der;‘;iParameter waren folgende: PeB>ca. 1,004, %||S 80, F^TOl,    woraus sich für £_{0 5} ergeben würde:

lilÉn w • 2,05 • 0,69 Bo,00007 Sekunden oder    Sekunden.

80    14000

Diese Bestimmungen ha®®ur groben ®lhep^^ Was sie zeigen, is| znnaqhst, daß die B^^hnuns auch für extreme Werte der Parameter :£o$endi^ungSHQQâßiig brauchbar bleibt. Ferner, daß man durch entsprechende Dimensionierung von der Geschwindigkeit der Auffüllung des

³ Unveröffentlicht® Versuche.

Abb. 7 . Einstellkur ve^^^ re -|j||pj^ trägheitsarmen Übertragung (benützt; zur Registrierung des Bronchialwiderstands ankleinenTieren (Lopèz, 1952).

12 Helv. Physiol. Acta 10, 1915,2

182

W. Wilbrandt, J. L. de la Cuadra und F. N. Witt

Abb. 8. Trägheit einer pneumatischen Übertragung mit, extremen*jParaime^erwerten. Die Ordinaten sind die optisch registrierten (bzw. ausgemessenen) A.miBëiir’ hei pneumatischer Übertragung verschieden frequenter“ Schwingungen    ân,

Benützt wurde die Membran eines von einem Frequenzgenerator (Philips)^t4g^^^illen ‘ * LaütsprëGher^. •

Raums II praktisch weitgehend unabhängig werden!* ‘kann. Damit ist. gemeint, daß dann limitierende Eigenfrequenzen auf treten Werdetiy TÉëlföé die Auffüllung zu langsam wird. Die Probleme dér Träghfp sind äaühÄb gleichen wie bei den üblichen direkten Registrierungen. *

Zusammenfassung Die Trägheit der pneumatischen Druckübertragung bz,w. Druckverstär-kung wurde durchgerechnet. Als Maß wurde gewählt die Hälbanstiegszeit, d. h. die Zeit, zu der nach einem plötzlichen Anstieg des primären |zu.übertragenden bzw. zu verstärkenden) Drucks der sekundäre Druck sich um 50% der totalen Druckänderung verschoben hat. Die Hälbanstiegszeit èr-

weist sich, als abhängig von vier Parametern: dem Volumen V des aufzufüllenden Raumes, der Volumnachgiebigkeil (reziproke Volumelastizität) dieses Raumes (&;==;dV/dP), der Strömungsgeschwindigkeit v des Luftstroms und der Größe der totalen Druckänderung A P:

A P    ,

• 0,69. (Vereinfachte Form der entwickelten Beziehung.)

Die abgeleiteten Gleichungen wurden experimentell geprüft, wobei sich befriedigende Übereinstimnäii* ergab.

Bei extremer Wahl der Parameterwerte können nach der Berechnung Halbanstiegszeiten bis zur Größenordnung von Viooo und Vioooo’Sekunden erreicht werden. Experimentell konnte gezeigt werden, daß optisch unter solchen Bedingungen Frequenzen bis übegl 300 Hertz ohne Amplitudenverlust übertragen werden können. Praktisch wird diese Einstellgeschwindigkeit ® mechanischer Registrierung nicht ausnützbar sein, weil die Eigehfrequénzëif der registrierenden Apparatur tiefer liegen.

Summary

A calculation of the inertia in pneumatic pressure transmission and ampljgH f^caMÉt ist pMCeiited^ The criterion used is the half-time, t_0>5, defined as the time    for    development of 50%; of the total pressure change in

the secondary system after a sudden rectangular change in the primary system. The halftime is-a function of four variables: the volume F of the Space tol^ filled with air, the reciprocal volume elasticity of this space Bthe^^M|y4©f the^tr current v, and the value of the total pressure ^aBSiof^Ée secondary system, A P. Under certain simplifying conditions the function is:

■ if.(F + 4.0,69.

Experimental determinations are in good agreement with this equation.

If extreme values of the variables are chosen, half-times of the order of 0,001 and 0,0001 seconds are calculated. Experimentally under such conditions frequencies up to 300 c.p.s. were transmitted without loss of amplitude using an optical manometer. For practical purposes this velocity of adaptation may not be realizable because the limiting frequencies of mechanical recording systems will be lower.

Mechanische Druckverstärkung    183